Perfect Magic Cubes

The Successful Search for the Smallest Perfect Magic Cube

by Walter Trump

Abstract

Since 1866 the smallest known 'perfect' magic cube was of order 7. It was constructed by Andrew H. Frost.
Most magic cube experts thought that 'perfect' magic cubes of smaller orders do not exist.
In September 1st, 2003 I discovered a 'perfect' magic cube of order 6.
Together with my friend Christian Boyer from France I searched for a 'perfect' magic order-5 cube
and in November 13th, 2003 we finally were successful.
It is not possible to construct a 'perfect' magic cube of an order m with 1 < m < 5.

History of 'perfect' magic cubes

order	exists	disproved or discovered by	date
3	no	John Hendricks *	1972
4	no	Richard Schroeppel	1972
5	yes	Walter Trump Christian Boyer	November 2003
6	yes	Walter Trump	September 2003
7	yes	Andrew H. Frost	1866
8	yes	Gustavus Frankenstein	1875
n>8	Single Solutions were found by several authors
2k>4	yes	General solution by Mitsutoshi Nakamura	July 2004

* probably the first disproof was already done before

Definitions

A 'perfect' magic cube of order m > 1 is a m×m×m-array of the numbers from 1 to m³, where the sum of m numbers along any straight line equals the magic constant S = m·(m³+1)/2 .
There are 3m²+6m+4 straight lines: m² rows, m² colums, m² pillars, 6m diagonals (= short diagonals) and 4 triagonals (= long diagonals).

In a (simple) magic cube the sums of the numbers in the diagonals may differ from S.

According to John Hendricks the expression 'perfect' should be reserved for magic cubes that are pandiagonal and pantriagonal. Therefore Harvey Heinz (the author of the 'Magic Squares Lexicon') calls such cubes diagonal magic (suggested by Aale de Winkel).
Today I would prefer the term strictly magic cube, this term can be expanded on hypercubes of any dimension.

In a 'perfect' magic cube each of the 3m orthogonal planes contains a (non-normal) magic square.
There is an interesting subgroup: Cubes where all squares in the surface planes are magic.
Let us call such cubes s-magic cubes (s = surface).
Of course each 'perfect' magic cube is s-magic.

Order 3

There are only four magic cubes of order 3. They all are associative.
The 3 squares in the center planes are magic.
The squares in the surface planes are not magic.
There are no s-magic cubes of order 3.
We can even prove that non-normal s-magic cubes of order 3 are impossible. (In a non-normal cube the integers are not consecutive.)

Assume a square in any surface plane would be magic.
We show that the integer e in the center cell must equal S/3.
Considering the center column and the two diagonals we can write:
(b+e+h)+ (a+e+i)+ (c+e+g)= 3S
Bring the terms in another order:
(a+b+c)+ (g+h+i)+ 3e=3S
Since the rows are magic we can conclude: 3e=S
But only one of the 6 magic squares in the different surface planes can have S/3 in its center cell, because each integer may occur only once.
Thus it is impossible to construct a s-magic order-3 cube.

Order 4

I estimate that there are about 7·10¹² magic cubes of order 4. Amoung the plane symmetrical cubes I found 8 cubes that contain 6 magic squares and additionally one oblique magic square. All in all each cube has 14 magic diagonals.
See spreadsheet for more details: nearly-diagonal-4.xls
6 magic squares would be enough to build a s-magic cube. But the above mentioned cubes have at most 4 magic squares in surface planes. They are not s-magic.
Richard Schroeppel proved in 1972 that diagonal magic (= "perfect") cubes of order 4 are impossible. His proof can be generalized in order to prove that there are no s-magic cubes of order 4. See the complete proof (word document).

In January 2004 I found a cube that is really close to a perfect magic order-4 cube. All its orthogonals and diagonals are magic, only the four triagonals are not. This cube was published in March, 2004 in 'Spektrum der Wissenschaft', the German edition of 'Scientific American'.

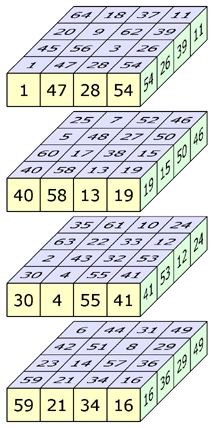
Three aspects of the nearly perfect magic cube of order 4 Walter Trump - January 2nd, 2004


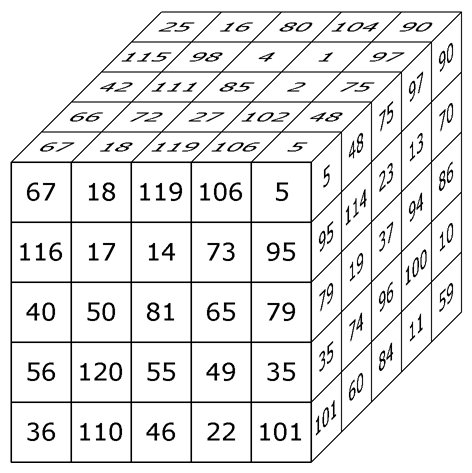
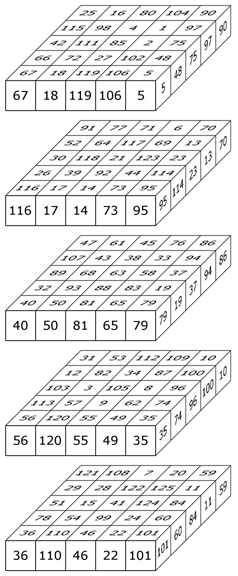
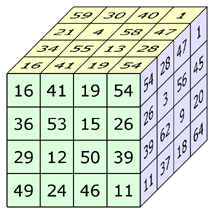
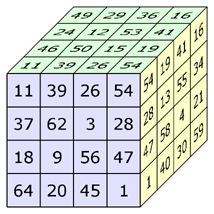
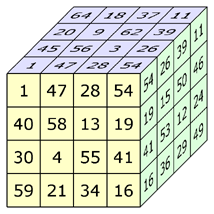
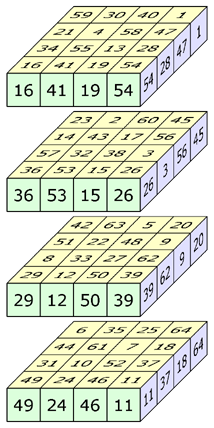
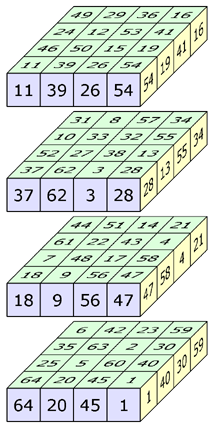
The 16 rows, 16 columns, 16 pillars and 24 diagonals are magic (sum = 130). The 4 triagonals have the sums: 100, 120, 140 and 160. Each of the 12 orthogonal planes contains a (non-normal) magic square.

Order 5

Do s-magic cubes of order 5 exist? The answer is YES.
In June 21st, 2003 I found such a cube.
Also another property of this cube is new: The cube is concentric (or bordered).
The 27 inner cells build an order-3 cube with consecutive numbers from 50 to 76.
See spreadsheet s-magic-5.xls
Unfortunately it is impossible to construct a bordered 'perfect' cube of order 5.

Do 'perfect' magic cubes of order 5 exist?
As far as I know, all experts for magic squares and cubes said 'No'. But the correct answer is YES.
In Summer 2003 Christian Boyer and I started to search for the impossible 'perfect' cube.
June, 2003: Christian Boyer found cubes with 22 correct diagonals by modulo 5 computations (*).
Then I created a backtracking computer program to find cubes with at least 26 magic diagonals. This program uses non-magic auxiliary order-3 cubes for the 27 inner cells.
July, 2003: First magic 5x5-cube with 26 magic diagonals.
September 18th, 2003: First order-5 cube with 28 magic diagonals.
Together with Christian Boyer I successfully improved the program. We also made changes in the list of auxiliary cubes and searched for the most promising ones. The program was now running on five computers (2 belong to my adult son Daniel).
October 26th, 2003: 28 magic diagonals and a difference of only 1 between a wrong diagonal and the magic sum
November 13th, 2003: First 'perfect' order-5 cube found by the computer of Daniel Trump: perfect-cube-5.xls
November 14th, 2003: Two other 'perfect' order-5 cubes found by computers of Christian Boyer and Daniel Trump.

The first known perfect magic cube of order 5 Walter Trump and Christian Boyer, 2003-11-13
This cube consists of all numbers from 1 to 125. The sum of the 5 numbers in each of the 25 rows, 25 columns, 25 pillars, 30 diagonals and 4 triagonals (space diagonals) equals the magic constant 315.

From Martin Gardner's point of view (see Scientific American, January 1976) the 'perfect' magic cubes are the only real magic cubes. Therefore this cube is of some importance for the theory of magic cubes. Its main property is that all (unbroken) straight lines are magic.

(*) Later I recognized that the cube of Dr. Theodor Hugel (Germany) also contains 22 magic diagonals. He published this cube in his book "Das System der magischen Figuren", 1875. Take a look at Hugel's cube and see that I learned from him how to visualize magic cubes.

In November 2012 H. B. Meyer (Germany) could prove that perfect magic 5x5x5-Cubes can not be central-symmetric (= associated).
Read more on Meyer's Homepage www.hbmeyer.de or look at my version of his proof: no-sym-perfect-5x5x5-cubes.pdf

Order 6

Harvey Heinz told me that a cube of order 6 found by John Worthington in 1910 can easily be transformed to an s-magic cube.
See worthington.xls

Until September 1st, 2003 a diagonal magic cube of order 6 was not known and most magic cube experts thought that such a cube would not be possible.
But then I found a 'perfect' order-6 cube: perfect-6.xls
To determine the cube I used a magic auxiliary order-4 cube with numbers from 1 to 32 and from 185 to 216. A usual PC found the result within a few minutes. Even computers from 1980 would have been able to do this job.

Order 7

A 'perfect' magic cube of order 7 is known since 1866.
It was one of the remarkable results of A. H. Frost: frost.xls

How did Frost constructed his cube?
He extended a method that was created by Leonhard Euler in order to construct magic squares.
This method does not work for smaller orders than 7.
! Therefore the construction of smaller perfect magic cubes is much more difficult and can't be done without computer.

Order 8

The first 'perfect' magic cube of order 8 was constructed by Gustavus Frankenstein in 1875.
Christian Boyer provides more details about this and other cubes: http://www.multimagie.com

Order > 8

Order 09: Charles Planck (1905)
Order 10: Li Wen (1988)
Order 11: Frederick A. P. Barnard (1888)
Order 12: William H. Benson (1981)
...
According to Christian Boyer (http://www.multimagie.com)

Order 2k > 4

In July, 2004 Mitsutoshi Nakamura from Japan sent me a bordered diagonal (='concentric perfect') cube of order 16. This cube contains 'perfect' cubes of order 6, 8, 10, 12, 14 and 16 with consecutive numbers.
Nakamura says that such a cube can be constructed for any order 2k > 4. And still in July, 2004 he published a bordered diagonal cube of order 40 at his web site: http://homepage2.nifty.com/googol/magcube/en/