
Number of magic squares
NEW 2024-05-31: Hidetoshi Mino succeeded now in calculating the correct number of magic 6x6-squares.
The results of historical and computer enumeration of magic squares
| Notes on Magic Squares and Cubes |
| by Walter Trump |

|
There are more magic squares of order 10 than elementary particles in our universe and in trillions of other universes (if they exist). Number of magic squares NEW 2024-05-31: Hidetoshi Mino succeeded now in calculating the correct number of magic 6x6-squares. The results of historical and computer enumeration of magic squares |

|
Magic Cubes as extensions of magic squares to 3 dimensions. Perfect magic cubes NEW 2024-06-20: Holger Becker discovered that a perfect magic cube of order 7 was already published in 1833 by Ferdinand Julius Brede alias de Fibre. Read about the fascinating features and the exciting history of these magic objects. |
|
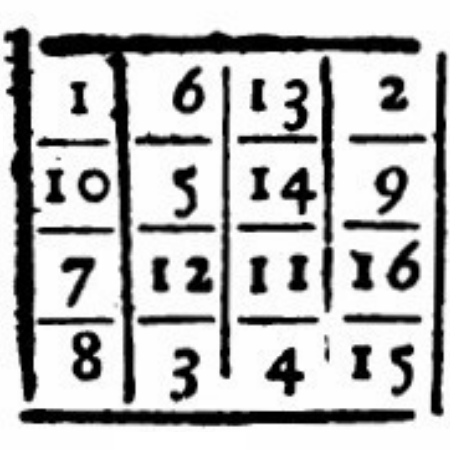
"quadrata subtractionis" published by Adam Kochański (Poland) in 1686. Magic Squares of Subtraction The old paper "Considerationes quaedam circa Quadrata et Cubos Magicos" was rediscovered by Henryk Fukś (Canada) and translated from Latin to English. |

|
Trimagic 12x12-squares are known since 2002-06-08. Trimagic Squares of order 12 Here some new squares with special properties are presented. For example: a trimagic square for the 60th anniversary of LEGO. |
|
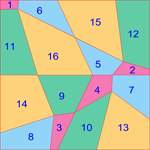
Graphic interpretation of magic squares Area Magic Squares Each area size is equal to the associated entry of the magic square. Area magic squares were first suggested by William Walkington in December 2016. |
|
Bimagic squares are still magic when all entries are squared. All bimagic squares of order 8 There are exactly 192·136,244 = 26,158,848 bimagic 8x8-squares. |

|
Ultramagic squares are both pandiagonal and centrally symmetrical. Ultramagic squares of order 7 Properties, transformations and beautiful examples of these squares. Read how to determine all 20,190,684 different squares. |

|
2 + 8 + 9 + 15 is a magic (trimagic) series of order 4. Magic series For orders m≥1000 the amount of series is very huge. Nevertheless exact enumerations could be done. Read all about these building blocks of magic objects. |

|
How many magic squares of higher orders are there? Estimates of the number of magic squares (cubes, hypercubes) Magic series and probability considerations enable us to estimate the numbers of magic objects. |

|
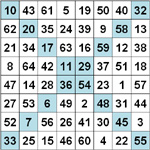
Strategy and source code of a special approximation Number of classical magic order-6 squares Learn about the Monte Carlo backtracking algorithm. |
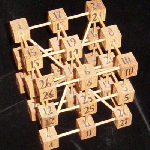
|
Links to great sites about magic squares and cubes Each of these sites covers the subject very completely and contains many further links. |