estimates - C-factor

Estimates of the number of magic squares, cubes, ... (hypercubes)

The C-factor

The E-number can be calculated exactly or at least with high accuracy.
But the E-number of certain magic squares (cubes, ...) is not exactly equal to their total number.
The aberration shall be described by a correction factor: the C-factor

Definition
Consider magic hypercubes (squares, cubes, ...) of order m and dimension n with certain magic properties.
Say N is the total number of these magic objects and E their E-number.
Then the correction-factor C is defined as C = N / E .
So we can write:

N = C · E

Number of magic squares, cubes, ...

For magic squares and semi-magic squares of orders up to 20 we already have got approximations by Monte Carlo methods with a relative error smaller than 0.5%. This enables us to approximate some C-factors.

The C-factor increases constantly up to order 17 and can be approximated by the linear function C_~(m):

C(m) ≈ C_~(m) = 0.185 · (m - 1)

C-factor approximation for magic squares with m ≥ 6

For semi-magic squares we may assume:

C_s(m) ≈ C_s~(m) = 0.1805 · (m + 1.5)

C-factor approximation for semi-magic squares with m ≥ 6

Note that the magic-series-method (E-number) does not really work for orders smaller than 6. There are too much symmetries and special properties of these magic squares. Thus there are more magic squares than we would expect by our statistics.

The following diagram shows the C-factors for magic squares (red) and semi-magic squares (yellow) together with their linear approximation functions.

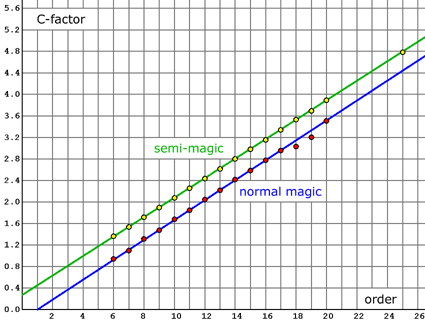
Click on the diagram in order to enlarge it.

The nearly linear increase of the C-factor for orders <18 is an experimental result. I haven't got a good analytical explanation.
Probably the C-factor increases slower for orders > 17. Further approximations with Monte Carlo methods would be necessary.

For orders greater than 20 we may assume that N(m) is greater than E(m) and smaller than C_~(m) · E(m).
Consider C_~(m) · E(m) as a slightly more accurate estimate for N(m) than E(m).

For magic squares of even orders the C-factor is slightly above the blue line and for odd orders below this line. The probability to be magic is lower for diagonals of odd orders because they share the number in the center.

The following diagram shows the differences between the C-factors C(m) and their linear approximations C_~(m).

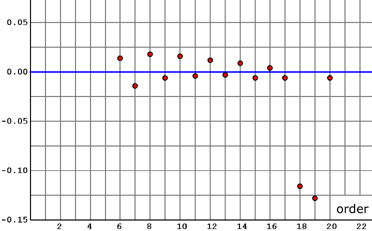
Click on the diagram in order to enlarge it.

I can't explain why the C-factors for order 18 and 19 are too small. This would mean that the diagonals must have a lower probability of being magic, because the number of semi-magic squares increases constantly. Probably there is a bug in one of my approximation programs. Or does anybody know why there are less magic squares of order 18 and 19 than expected?

Back to the Table of Contents