Ultramagic Squares of Order 7
Equations
25 equations from the self-complementary property
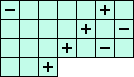
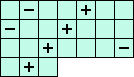
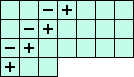
A magic square s is self-complementary if there exists a general square-transformation T (i.e. rotation or reflection) with C·T(s) = s.
Where C is the complementary-transformation, that changes the numbers of an order-7 square in the following way:
C:n(x,y)-->50-n(x,y) with natural numbers, or C:i(x,y)-->-i(x,y) with integers.
If the order of the square is odd, T has to be the 180°-rotation: T:i(x,y)-->i(8-x,8-y)
Proof: All axis reflections have 7 fixed cells that are in a row, a column or a main diagonal. But as C has only one fixed point, namely cell (4,4), C·T could not be the identical transformation.
We get C·T:i(x,y)-->-i(8-x,8-y) and as we consider self-complementary squares C·T:i(x,y)-->i(x,y).
==> i(x,y)=-i(8-x,8-y)
Let us use the shortform ixy for the integer i(x,y). We get 25 equations:

i15=-i73, i25=-i63, i35=-i53,
i16=-i72, i26=-i62, i36=-i52,
i17=-i71, i27=-i61, i37=-i51, 		i44=-i44, i54=-i34, i67=-i21, i74=-i14
i45=-i43, i55=-i33, i65=-i23, i75=-i13
i46=-i42, i56=-i32, i66=-i22, i76=-i12
i47=-i41, i57=-i31, i67=-i21, i77=-i11
The equation i44=-i44 is only fulfilled by i44=0.
If you know the 21 numbers of the first three rows and the first 3 numbers of the fourth row, you know the whole square. Thus we have to consider only 24 variables, the yellow part of the square.
Three row-equations
If the numbers in the first three rows sum up to 0, then also the numbers in the rows 5, 6 and 7 sum up to 0, because their numbers are negative to that in row 3, 2 and 1.
The sum in row 4 is automatically correct:
i14+i24+i34+i44+i54+i64+i74 = i14+i24+i34+i44-i34-i24-i14 = i44 = 0
The tables show a geometrical interpretation of the equations.
(A) i11+i21+i31+i41+i51+i61+i71 = 0
(B) i12+i22+i32+i42+i52+i62+i72 = 0
(C) i13+i23+i33+i43+i53+i63+i73 = 0
(A) (B) (C)
Three column-equations
The sum of the numbers in the columns has to be 0. The sum of the middle column is 0 as a matter of self-complementarity. The reduced square has no complete column. Thus we have to replace some numbers with the negative symmetrically located number. This gives us 3 new equations:
(D) i11+i12+i13+i14-i73-i72-i71 = 0
(E) i21+i22+i23+i24-i63-i62-i61 = 0
(F) i31+i32+i33+i34-i53-i52-i51 = 0
(D) (E) (F)
Six diagonal-equations
The sum of the numbers in each main diagonal is automatically equal to zero. There are 12 broken diagonals left. But symmetrically located diagonals have equivalent equations. Therefore we get only 6 new equations.
(G) i21+i32+i43-i71-i12-i23-i34 = 0
(H) i31+i42+i53-i61-i72-i13-i24 = 0
(I) i41+i52+i63-i51-i62-i73-i14 = 0
(G) (H) (I)
(J) i61+i52+i43+i34-i11-i72-i63 = 0
(K) i51+i42+i33+i24-i21-i12-i73 = 0
(L) i41+i32+i23+i14-i31-i22-i13 = 0
(J) (K) (L)
Derived equations
Notice that we got an homogeneous equation system with 12 equations and 24 variables. Investigations show that the system is linearly independent, i.e. no equation is a linear combination of the others.
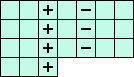
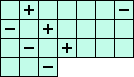
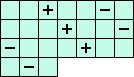
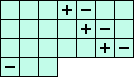
The following equations are linear combinations of the 12 fundamental equations A, B, ... K. But as these new equations contain only 6 variables they are very useful for the calculation of squares.
(M) i21+i41+i61+i32+i52+i43 = 0 <=> ( 3(A+G+J) +2(B+I+L) +1(C-H-K) ) / 7
(N) i41+i32+i42+i52-i13-i73 = 0 <=> ( 1(A+G+J) +3(B+I+L) -2(C-H-K) ) / 7
(O) i21+i61+i13+i43+i73-i42 = 0 <=> ( 2(A+G+J) -1(B+I+L) +3(C-H-K) ) / 7
(M) 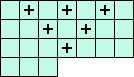(N) 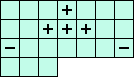(O)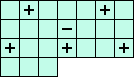
(P) i11+i21+i31+i12+i22+i13 = 0 <=> ( 3(A+D-L) +2(B+E-K) +1(C+F-J) ) / 7
(Q) i21+i12+i22+i52-i33-i63 = 0 <=> ( 1(A+D-L) +3(B+E-K) -2(C+F-J) ) / 7
(R) i11+i31+i13+i33+i63-i52 = 0 <=> ( 2(A+D-L) -1(B+E-K) +3(C+F-J) ) / 7
(P) 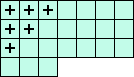(Q) 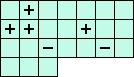(R)
You can easily generate more equations by rotating the squares. Thus you get 24 such equations. They were all generated by applying special transpositions with equation (M).
Index
summary cells equations transpositions improvements
results programs files conclusions samples
Walter Trump, Nürnberg, Germany, (c) 2001-04-25 (last modified: 2004-06-27)